病毒性如同病毒
我们继续发布由Wooga市场部负责人Eric Sёufert撰写的《Freemium法典》系列文章。今天轮到的是分析公司Feastie创始人Valerie Coffman的文章。
最佳病毒营销数学模型
现代商业社区的病毒营销模型基于错误的假设。因此,这些模型无法反映实际情况。
那么,商业社区如何建立一个现实的病毒营销模型呢?如何识别最重要的因素(病毒系数、时间范围、用户流失、市场规模)?幸运的是,我们有大量关于病毒增长(和衰退)数学模型的文献,这些研究始于1927年。这些模型在讨论市场规模变化和以前用户再次回归的可能性时非常合适。显然,在那个时候没有人会想到YouTube视频或iPhone应用,那个时代的电话还在用有线和拨号盘。这些模型描述的是…病毒的传播。
模型
经典的SIR疾病传播模型是由Kermack和McKendrick提出的。我将其应用于病毒营销,进行疾病与产品之间的类比。其结果当然大相径庭,但数学是一致的。
Kermack和McKendrick将市场上的总人口N分为三组。
- S – 对疾病感兴趣的人数(潜在客户);
- I – 患病的人数(现有客户);
- R – 康复的人数(曾经的客户)。
这些人群的数量随着时间的推移而变化。潜在客户通过成功的邀请转为现有客户。现有客户若停止使用产品,则成为曾经客户。为了简化,我将市场的总规模N=S+I+R视为一个常数,而将曾经的客户视为获得免疫力的人。控制疾病传播的参数包括:
- β – 感染速度(交换率);
- γ – 康复速度(流失率)。
假设现有用户I与潜在用户S之间的互动频率与他们的数量成正比(这由有效能量法则控制)。因此,从口碑传播或社交网络分享中获得的新用户数量可表示为 βSI。我们的用户数量增加了βSI,而潜在用户数量减少了同样的数量。这与Skoch模型中的“病毒系数”发挥着同样的作用,同时也解释了当试用产品的人数增加时,分享转化率减少的现象。此外,我们放弃了“时间周期性”的概念。相反,我们采用平均分享所需时间和人们分享的平均频率,这在β的分母中计入时间单位。因此,β代表了当前用户在单位时间(例如小时、天、周)内成功邀请潜在客户的次数。我认为这比Rais和Skoch使用的病毒系数的定义更为可靠,因为根据时间的平均模型化病毒交换导致以下事实:
- 用户不会在同步批次中分享;
- 每个用户需要时间来尝试产品、爱上它并与朋友分享。与其对所有人设定相同的循环时间,不如说β表示平均交换速度;
- 用户可以在首次尝试时邀请其他人,或者在使用一段时间后再邀请。
在此模型中,现有用户成为曾经用户的速度由参数γ确定。因此,γ是单位时间内转为曾曾用户的现有用户的比例。它与时间成反比(1/t),1/γ是用户作为用户的平均持续时间。因此,如果γ=1%(每天有1%的用户流失),那么用户的平均生命周期为100天。
病毒传播的微分方程:
- dS/dt=−βSI
- dI/dt=βSI–γI
- dR/dt=γI
分析方程
这是无法方便地解决以获得S(t)、I(t)和R(t)公式的非线性微分方程。不过,它们可以显示动态(特别是市场规模和返回消费者的变化)。通过研究它们并进行数值积分,您可以了解很多。我们假设t=0代表新产品的发布。起初,只有开发者才代表消费者,并且是用户基础I(0)。最初的曾经消费者数量R(0)=0,而其他人则是潜在客户S(0)。
首先需要注意的是,当dI/dt>0时,用户基础在βS/γ>1的情况下增长。
换句话说,只有当针对市场S(0)的规模和交换速率β大大超过流失速率γ时,病毒增长才能发生。模型显示,即使在较小的β下,只要市场规模足够大,您仍可以体验到病毒增长,只要流失率也不高。
如果在t=0时S的数量非常接近N,则βS/γ大约等于βN/γ。因此,如果βN/γ>1,则用户基础将增加;如果βN/γ<1,则不会。这个在流行病学文献中有时被称为“基本再生数”。重要的是,正如Eric Rais所称的“病毒系数”也依赖于市场规模和用户流失率,它与病毒交换速率一样。这大约是每个用户在整段时间内邀请的新客户的平均数量,正因为如此为1/γ。然而,在病毒增长的情况下,βN/γ很快就不再代表每个用户邀请的客户数量。
从这些方程中,您还可以看到如果忽略市场规模的变化(这在短命的病毒产品中是合理的,比如YouTube视频),用户基础在较长的时间内总是会收敛到0,除非您的流失率等于0。一旦现有用户数量达到峰值dI/dt=0时I=N–γ/β,用户数量的变化速度将变为负,最终会降到零。这与Mashable关于Twitter和YouTube帖子的半衰期的数据相一致。再次注意流失在确定客户峰值中的关键作用。
示例
我们可以通过数值积分这些方程来更深入地了解。例子中时间单位为β和γ是天,不过您可以选择任意。为了更贴合Rais对病毒系数的概念,我将β定义为βN——如果在t=0时S(0)大约等于N,则βN代表每位现有用户每天可以触及的新用户数量。
设定:
N = 市场上100万人。
βN = 用户每天发出10个邀请
γ=50%用户每天流失
I(0)=10个初始用户
通过数值积分上述方程,我们将得到在首30天内用户数量变化的图景:
该图类似于流行推文的传播情况,流量会快速增长然后下降,因为人们对主题感到厌烦。
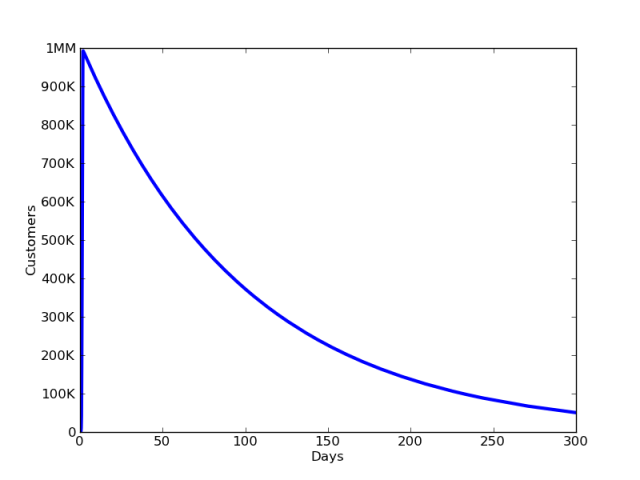
对于流失率较低的情况,即γ=1%用户每天流失,我们在300天内看到以下图景:
这表明,即使在流失率较低的情况下,如果没有新潜在用户进入市场,或没有曾经客户返回,用户基础在达到峰值后始终会减少。还要注意,更低的流失率使我们在流量中获得了更高的峰值。
那么,如何维持持续的病毒增长呢?您需要理解病毒营销如何影响市场规模的变化。
本文是由移动开发网站App2Top.ru和Apptractor.ru合作推出的“Freemium法典”系列的部分内容。
原创材料:http://datacommunitydc.org/blog/2013/01/better-science-of-viral-marketing-part-2/