LTV和留存率曲线的分析与工作

关于如何构建LTV和留存等指标的函数，Overmind工作室的总制作人伊万·伊格纳托夫（Ivan Ignatov）进行了详细讲解。注意：有很多公式。

伊万·伊格纳托夫

任务设定

对于游戏应用程序的用户获取（User Acquisition）领域中的大多数分析任务，以及与游戏设计中的经济计算相关的任务，往往依赖于项目的关键指标，即留存曲线和LTV曲线。

留存曲线r(t)是一个函数，反映了自用户注册以来，留在项目中的用户比例与时间的关系。例如，如果在注册后的第7天仍然保留10.7%的用户，而在第10天为8.8%，那么可以说第7天的留存率为0.107，第10天的留存率为0.088。也就是说，r(7) = 0.107，r(10) = 0.088。

LTV曲线L(t)是一个函数，反映了自用户注册以来，每个玩家产生的平均收入随时间的变化。例如，如果在注册后的一个月内，用户平均带来2.55美元的收益，则可以说“LTV 30为2.55”。也就是说，L(30) = 2.55。

通常，使用LTV这一缩略词并不是指L(t)函数本身，而是指“用户生命周期内的总收入”这一数值，即L(∞)。由于这个值通常仅适用于很早就存在的应用程序，而此时分析已经为时已晚，因此在实践中常常使用六个月或一年的平均收入，即L(182)或L(365)。例如，“流量在六个月内必须收回成本”这一说法意味着L(182) ≥ CPI。

在许多情况下，有必要构建r(t)或L(t)的分析表达式，即根据项目的统计数据“写出公式”。换句话说，用分析曲线来逼近统计数据。

此类任务的示例包括：

• 为尚未达到相应年龄的项目预测几个月后的留存率和LTV；
• 评估平均用户的LT（生命周期）；
• 根据广告活动开始后几天的结果评估广告流量的回报率；
• 游戏设计师构建一个经验等级的尺度，使所有等级的玩家数量大致相同；

以正确的方式接近问题

当分析师面临构建此类公式的必要性，或至少从网络上现有模型中选择时，以下几点是很有用的。

我们每个人都知道许多明显的公理，例如“所有用户迟早会离开项目”、“用户的平均生命周期不能无限长”、“从注册开始时间越长，留存用户的比例越低”，甚至“在注册时每个用户都是活跃的”等等。

但并不是每一个用于逼近r(t)或L(t)的公式或模型都能通过这些“显而易见的真理”进行验证。

例如，有时留存模型使用的是双曲线：

当C > 0时，它会给出一大群从未放弃应用的用户。

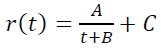
作为LTV模型，有时也使用所谓的“幂趋势”L(t) = At^B，它简单地假设如果考虑“用户的生命周期”，LTV是无限的。

这导致所选模型往往无法很好地逼近现有数据，或者在特定时间范围内可以，但是当被要求进行几个月的预测时，它开始出现问题。

接下来，我将描述一种基于研究所需函数的自然特性的“写公式”的方法。其核心是从所有可能的公式中选择那些属性与我们关于项目受众行为的经验看法相匹配的公式。这不仅仅是对最简单的看法“显而易见的真理”的符合，还有更复杂的看法。比如，“用户在项目中呆的时间越久，今天他离开的可能性就越小。”

留存与LTV之间的关系

在直接解决问题之前，需要注意，LTV曲线的形式的查找可以归结为留存曲线类型的查找，因此将两个不同的任务视为一个任务。可以这样进行。

LTV的时间导数L`(t)代表着平均用户在单位时间内的累积收入，从本质上来说与留存曲线r(t)相近。而且，当活跃玩家A的单位时间内收入固定时，它们之间是成比例的：L`(t) = A r(t)。

在市场营销中，A通常被称为ARPU（每用户平均收入）。不幸的是，ARPU有时也被理解为其他的。例如，L(30)常被称为“第一个月的ARPU”。但在我们的工作中，ARPU将被具体理解为在单位时间内每个活跃玩家的平均收入，别无他意。

往往在第一近似中，A被假定为常数，与用户的年龄无关，因此L`(t)和r(t)按相同的法则变化。实际情况是，未付费用户通常比付费用户更早放弃游戏，因此A根据用户的游戏时间而增长，即t。换句话说，A = A(t)且L`(t) = A(t) r(t)。

但即使在这种情况下，A(t)也保持类常数，变化缓慢，相较于L`(t)和r(t)。这为我们寻找它们变化的公式提供了依据，并在同一族的曲线中。

这种方法得到了应用，且其有效性通过实践证明，得出的平滑曲线L(t)与考虑的项目的原始经验LTV曲线相当接近。

推导所需的曲线

因此，我们将推导r(t)。这个过程遵循什么样的法则，具有什么“自然特性”？

首先列出我们之前归类为“显而易见的真理”的特性：

1) r(0) = 100% = 1（在注册时所有用户都活着）
2) r(t)在[0 ; ∞)区间内递减（平均而言，用户会放弃游戏）
3) ∫₀^∞ r(t) dt是有限的。

这意味着什么，“积分是有限的”？

假设稳定项目的流入流量为N人每单位时间（每天）。

那么在项目中，年龄从t到t+h的玩家数量是N r(t) h，项目中的活跃玩家总数是所有这些数量在整个玩家年龄轴上的总和，以步长h表示，即：

实际上我们知道，即使在持续很长时间均匀注入流量的情况下，它的活跃受众人数也不会无限增长，而是会达到一个固定的“平台”，而要突破这个平台则需要更多的流量，即增加N。这意味着M是有限的，因此考虑中的积分是有限的。

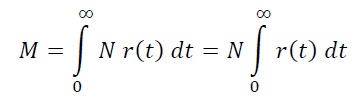
顺便说一句，可以清楚看到，用户的平均生命周期：

这个声明可以通过更严格的推导得以确认，从数学期望的概念和密度f(t)定义的事实出发，发现玩家在项目中的生命周期分布为f(t) = -r’(t)。

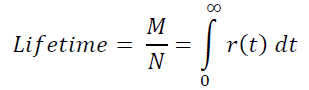
满足属性1) - 3)的最简单初等函数为r(t) = e^-αt, a > 0。

然而在尝试使用该家庭函数时，我们遇到以下情形。实际经验留存率在年龄轴的早期迅速下降，之后缓慢下降。

这意味着在一开始，即在注册后不久，玩家比根据r(t) = e^−αt的法则更快地离开项目，而在游戏中呆了几个月后则慢下来。

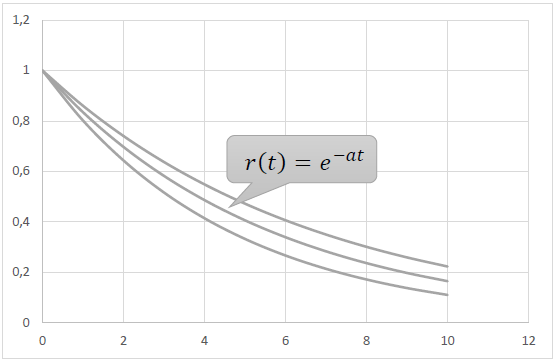
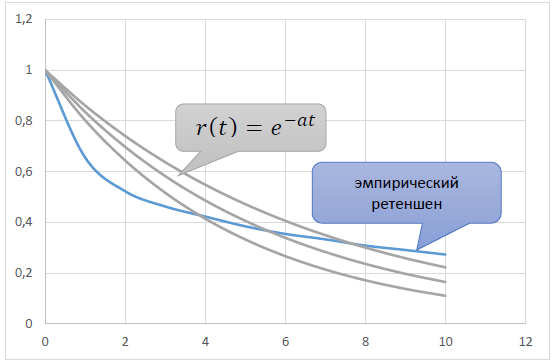
这种行为可以用留存的以下经验性质来解释：

4) 从注册时起，时间越长t，流失“概率”p(t)越低。

“流失概率”是指用户在下一单位时间内离开游戏的概率，假设他之前并未这样做。

p(t)和r(t)之间有什么关系？

假设我们有N玩家在每单位时间的流入流量，那么到达年龄t的玩家数量为N r(t)，到达年龄t+h的玩家数量为N r(t+h)。

因此，在年龄区间[t ; t+h]，有N r(t)− N r(t+h)玩家流失。这意味着，在h时间内，项目流失的比例为

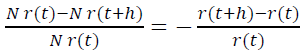
需强调的是，这里的时间是指玩家从注册开始的主观时间，而不是所有玩家的一个客观的公共时间间隔。那么在单位时间内，项目流失的比例为

由于该比例等于考虑的流失概率，因此：

回到经验法则4)，根据该法则p(t)是递减的，我们来看它如何在r(t) = e^-αt的法则下表现。

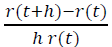
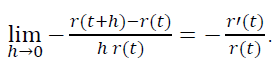
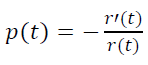
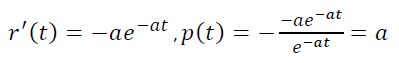
也就是说，模型中的p(t)是常数，而不是递减。因此观察到的经验r(t)和模型r(t)=e^-αt之间存在这种差异。

我们尝试概括模型，使得p(t)递减。

设p(t) = αt^β

• 当β = 0时，我们得到前面讨论的模型p(t) = α，r(t) = e^-αt
• 当β < 0时，我们得到所需的递减流失概率。
• 当β > 0时，我们得到一个奇怪的应用情况，随着玩家生命周期流失概率增加。例如，一款内容时间限制较严的游戏。

根据新的模型：

如果β ≠ −1，则

此时r(0) = 1，因此e^C = 1，也就是说：

重新定义β+1 = b，α/(β+1) = a，得到留存模型：

公式 *

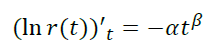
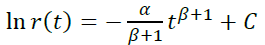
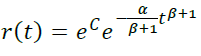
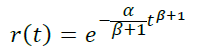
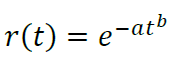
• 当β < 0 ⇔ b < 1（流失递减，正常情况）
• 当β = 0 ⇔ b = 1（固定流失，简单的指数模型）
• 当β > 0 ⇔ b > 1（奇怪应用情况，流失率增加）

通过调整参数a和b，以接近理论r(t)与经验留存之间的要求，可以得到一个足够准确地反映现实的模型曲线：

相应地，LTV曲线应用相同的法则L′(t)=Ce^−αtb，这在积分时给出以下公式：

公式 **再通过u齐分析，可以得到接近实际的LTV模型曲线。任务已经完成，最后可以给出一些小的附加说明。

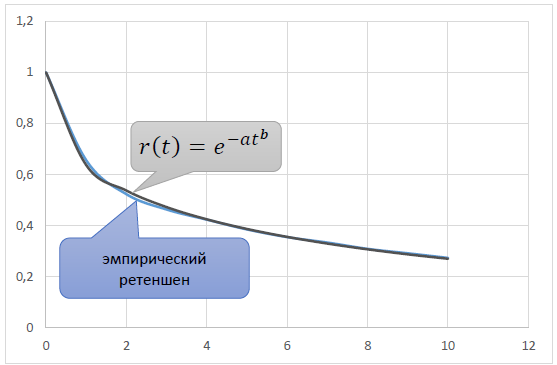
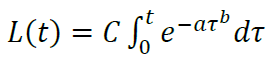
第一次说明：关于幂趋势

属性3）意味着r(t)的受众有限，且对于L(t)，LTV也是有限的，仅在β > −1，即b > 0时满足。

如果考虑同样的模型p(t) = αt^β当β = −1时，得到：

r(t) = Ct^−α – 幂函数，无法取值r(0) = 1，并且当α < 1时在无穷大处不可积，然而这种情况下相应的模型是：

最后的函数是幂函数，这便是市场营销人员常用来逼近LTV曲线的“幂趋势”。

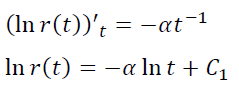
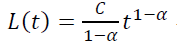
结论：对于LTV曲线，虽然幂趋势不满足模型(**)的条件1)和3)，但仍然是其极限特例，当b → −1时，同时a → ∞。因此，就算市场营销人员使用“幂趋势”并认为其与LTV曲线的行为相关，那么模型（**）同样可以被认为是相关的。

第二次说明：关于增加参数的数量

如果分析师拥有大量统计数据，他可能会希望将逼近曲线调整得更接近，期望这样能得到更精确的预测。

此时，他准备在模型中增加更多的额外参数。例如，构建r(t)不是我们的双参数模型（*），而是三、四或五个参数。

如何在框架内满足该要求呢？

可以对玩家进行混合建模。假设我们的流量由两种用户混合而成，权重为p和1−p，每种类型都有自己的参数 – a₁,b₁和a₂,b₂。那么就能得到：

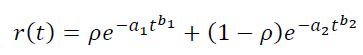
同样可以在LTV模型中增加参数数量：

如果需要更多参数，则可以使用三种及以上类型“用户”混合而成。

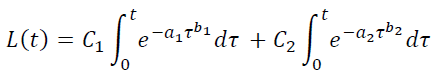
然而，使用多参数模型时需要非常谨慎。如果参数过多，分析曲线可能会适应随机波动和统计数据的起伏，并引导出实际不存在的趋势。在这种情况下，尽管多参数模型距离统计数据更近，但基于此得出的预测和其他结论则可能不够准确。

因此，在使用五参数模型之前，最好仔细考虑五次，这样做是否必要。

第三次说明：如何使用

为了实际应用找到的模型，需要掌握两件事。进行（**）形式的积分，以及找到最佳参数集合a，b，C。

这个积分无法用初等函数表示，但可以通过下不完全伽玛函数γ(s,x)进行变量替换，举例来说，可以在MS Excel中实现，通过实现的伽玛函数和伽玛分布公式为：=EXP(GAMMALN(s))*(GAMMA.DIST(x,s,1,TRUE))。

在MS Excel中也可以找到最佳参数集合。为此，可以编写目标函数，考虑到最小二乘法的方法，即理论曲线与统计数据的平方偏差之和。然后通过“求解”插件调整参数，选择“非线性规划法求解”的方法。

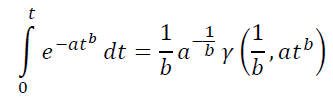
由此可见，为了使用所建议的模型，无需特殊软件或程序员的参与。

至此，所有内容都已完结。希望这对您有趣。如果有任何问题，请在评论中告知。