材料部分：平衡的逆向工程（第一部分）

安南金·谢尔盖，Pixonic公司制作人，撰写了一篇关于游戏平衡反向工程的引人入胜（巨型）文章。在作者的允许下，我们在App2Top.ru上发布这篇文章。我们强烈建议大家仔细阅读，但一定要做好数学和绘制图表的准备！

0. 关于文章的主题

在开发和发布一款游戏时，我们必然依赖于其他团队和项目的经验，无论是在游戏玩法的设计（例如，"Flappy Bird"的规则！）还是在选择吸引策略（例如，高病毒传播性 = 低获客成本，万岁《糖果传奇》）。

调控游戏难度并管理游戏中的经济周期的数学模型也不例外。在试图在自己的游戏中创造理想平衡的过程中，成功的一个关键因素是对类似成功项目的详细解析，以了解它们的数学本质——管理游戏经济和游戏玩法的一系列法则。然后可以在自己的项目中使用这些法则，并根据游戏的现实情况进行调整。我们所称的找出这些数学法则的过程就是反向工程（来自“工程”（即设计）和“反向”（即逆向）的组合）。

在这篇文章中，我们将努力弄清楚，反向工程到底是什么，它的过程是如何运作的，以及这一过程的结果和所产生的果实。

和往常一样，这篇文章并不是一个具体的行动指南，也不包含准确的法则，而是反映了我们在这个问题上的个人经验和我们对反向工程理解和实现的方式。

1. 关于公式和数字

假设我们有两个变量，其中一个依赖于另一个。例如，使用符号E表示玩家为提升到下一个等级所需获得的经验值，符号x表示玩家的当前等级。设E依赖于x（即，例如，在第一级时，玩家需要获得10点经验才能提升到下一等级，第二级，而在第五级时，需要100点经验才能提升到下一等级，第六级）。

E对x的依赖通常表示为E(x)，并称E为x的函数（因此E用大写字母书写，而x用小写字母书写）。这种依赖可以以两种形式表示：

• 连续形式，通过方程表达（例如，E(x) = x2）；
• 离散形式，通过表格（每个具体值x将对应一个值E）。

连续形式与离散形式的主要区别在于：如果函数以连续形式给出，则可以在任意参数值处获得其值（当然，如果该参数值的函数值在原则上是可计算的）。但这对我们意味着什么呢？

手头有函数的表格表示时，您只能知道在预选的参数值（在我们的示例中为x = 1, 2, 3, 4, 5等）下的值。如果您手中有方程，您不仅可以为相同的x = 1, 2, 3, 4, 5等确定函数值，还可以为其他任何值，例如x = -2或x = 3.75。在我们的级别和经验示例中，x = -2或x = 3.75没有意义（因为级别是正整数！），但是，请考虑一下：如果您的表格在x = 100处结束，而您需要知道玩家需要多少经验才能从101级提升到102级？要回答这个问题，您将需要一个方程。

最初，分析另一个（他人的）项目时，您只获得每个游戏中存在的函数的离散记录。假设在创建农场游戏时，您以这一流派的热门游戏的平衡为基础，一级接一等级积累，并记录下获取下一级所需的经验值。经过一百个等级，您将获得函数E(x)的离散记录——一张包含一百行的表格，每行对应每个从1开始的整数值x。

您对这份记录会产生许多疑问。例如：对于x = 150，E的值会是多少？这些数字是按什么原则选择的？随着x的增加，它们增长得有多迅速？这些数字的增长速度是增加还是减少？

这样，我们接近了反向工程的主要任务。项目数学的反向工程主要目的是揭示游戏中的依赖关系，其次是获得这些依赖关系的连续记录。揭示依赖关系将使我们了解哪些游戏变量彼此相关。获得连续记录（即方程）将使我们可以根据自己的意愿使用这些依赖关系，并根据我们的需要进行调整。

2. 离散化、逼近及其他

从连续记录转变为离散记录的过程实际上是非常简单的。手头有方程时，您可以依次将不同的参数值代入其中，从而获得相应的函数值。在我们的例子中，将x = 1, 2, 3, 4, 5等代入方程E(x) = x2，将获得E的值为1, 4, 9, 16, 25等。这个过程称为函数的离散化。

相反的过程（从值表获取方程），称为逼近，通常要复杂得多。这正是我们特别感兴趣的内容。在讨论如何进行逼近之前，让我们先明确一下，这么做的具体目的是什么。

使用正确的术语，可以列出应用逼近能够解决的以下任务：

• 插值，即获取函数的中间值（记住关于为x = 2.5找到E的例子，在级别的情况下意义不大，但在计算其他函数时，如果我们只有函数的表格记录，这可能成为一件麻烦事）；
• 外推，即获得初始描述范围之外的值（如果表格在x = 100处结束，而您需要找到x = 150的E，这个任务就需要解决）。
• 分析，即获取函数的行为信息（换句话说，就是获取正在发生的事情的全貌）。例如，知道E(x) = x2的情况下，我们可以对“下一个等级的经验增长”做出怎样的结论？显而易见的结论是：随着x的增加，E增长。这就是说，想要达到更高的等级需要更多的经验。一个不太明显的结论是：E的增长速度不仅为正，而且还在增加。这意味着，玩家越是进展，其所需的下一级经验增长的百分比就越大。在获取函数后，分析后也可以将其与其他函数进行比较，以便了解哪些函数增长得更快，哪些更慢，从而看到游戏的平衡如何随时间变化。

3. 揭示依赖关系

在逼近变得有意义之前，我们的第一个任务是揭示我们想获得连续记录的那些依赖关系。通常，游戏循环基于许多不同的简单和复杂的依赖关系。

在我们的示例中，E对x的依赖是一目了然。对于“农场”类型的游戏，达到下一级所需的经验值不太可能依赖于角色的当前装备或他朋友的数量。

在分析项目时，您会碰到更复杂的依赖关系。揭示它们的步骤约可总结如下：

• 形成可能依赖其他变量的游戏变量的初步列表（在我们例子中，商店中商品的购买价格可能依赖于其等级或特性；或者更复杂的情况——某些特性可能依赖于其等级，而价格则依赖于特性）；
• 形成一些可能并不依赖于任何东西，或者其形成法则相当清晰的游戏变量的初步列表（例如，下一等级的编号——总是从前一等级+1，而新等级的奖励——总是+1金币）；
• 列出所有可能的依赖关系（例如，物品价格与其级别的关系、物品价格与其参数的关系、物品级别与其参数的关系等）；
• 对这些潜在依赖关系进行初步研究，看看它们是否像依赖关系，还是看上去更像是随机数字的集合。

在列出潜在依赖关系以供研究时，重要的是不要害怕开始。克服恐惧的关键很简单：要记住，如果所选择的依赖关系根本不是依赖关系，其分析将会让您明白，您可以毫不犹豫地将其从列表中去除。

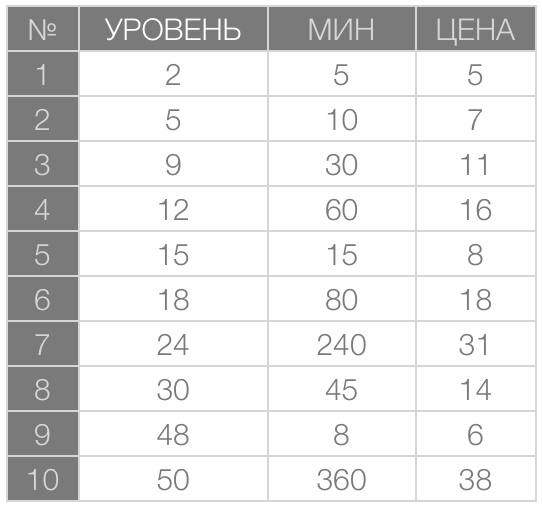
让我们更详细地讨论一下“初步研究”这一点，这应该引起最大的关注。考虑一个例子：假设在所研究的游戏中，需要种植植物并在自己的商店中出售它们。这些植物在不同等级可供种植，具有不同的成熟时间，并以不同的金额卖给玩家。这里可能有不同的依赖关系：售价和成熟时间可能依赖于这些植物可种植的等级，也可能相互依赖。

在描述的情况下，我会同时分析这两个选项。假设游戏中只有10种植物。每种植物的相关数据在下表中进行描述。

在这里，左列中给每种植物分配了一个序号（而不是名称）。在接下来的列中，给每种植物提供了它对玩家的可用等级、成熟所需的时间（以分钟计）和在商店中的出售价格。

我们尝试分析以下依赖关系：

• 时间与等级的关系；
• 价格与时间的关系。

您可能会笑，但我认为揭示依赖关系的最实用方法是根据其表格记录构建预期函数的图表。构建这样的图表很简单。我们选择表格中的两列，将它们按参数列中数值的升序排序，然后在x轴上标出参数列中的值，在y轴上标出函数列中的值。

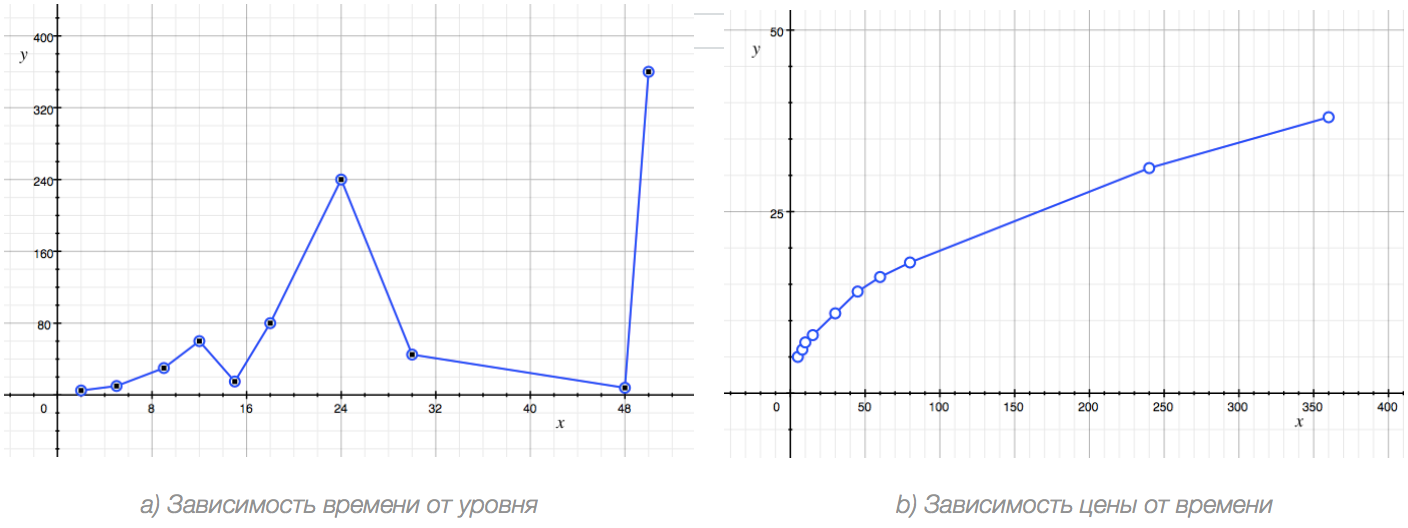
这是我们的结果。在左侧选项中，函数是列的MIN数值，而参数是列的LEVEL值。在右侧选项中，函数是价格，而参数是分钟列。

有很多不同的方式来逼近特定类型方程的表格记录，但如我所说，在实践中，最方便的方式是观察所构建的图表。为了理解所获得的图表是否代表函数，而不是随机的点集，可以简单地问自己一个问题：我能否在心里（哪怕只是理论上）将图形延续下去？我们看到，在a)的情况下，这几乎是不可能的（这里我们有折线，向上或向下波动，我们无法预测其行为）。而在b)的情况下，很明显，图形接着会上升，并且增长的速度会减慢。这意味着在a)的情况下，我们没有依赖关系，而在b)的情况下，存在依赖关系。

在开始逼近函数并充分利用图表之前，还需要注意另一个方面。请允许我做一个预测：即使您熟练地逼近数值集合，得到的函数也不会百分之百准确地再现表格数据。这有两个原因：

• 四舍五入。开发者所使用的公式在某种情况下并不会关心给予其数字的美观。因此，平方根2是一个有无穷多个小数位的数字。将这样的数字放入游戏中是不可能的，因此必须对其进行四舍五入。请注意，在小数字下，四舍五入会给数据带来特别大的误差。例如，平方根2（约等于1.4142135…）可以四舍五入到1.5，而如果游戏中必须是整数，则可四舍五入到1或2。在这种情况下，差距为1是非常重要的。例如，相差1的数100和101本质上只相差1%，而1和2之间则相差100%！
• 手动“调校”——反向工程中特别头痛的问题。开发者通常（而且这样做是对的）将应用的公式仅作为起始点，即他仅用其构建一版初步的平衡，随后根据个人直觉、游戏数据、玩家愿望等进行手动调整。经过手动调整的数字不仅可能与公式稍有偏离，甚至会让试图揭示原始法则的人感到困惑。为展示这一点，我们来看一个简单的例子。

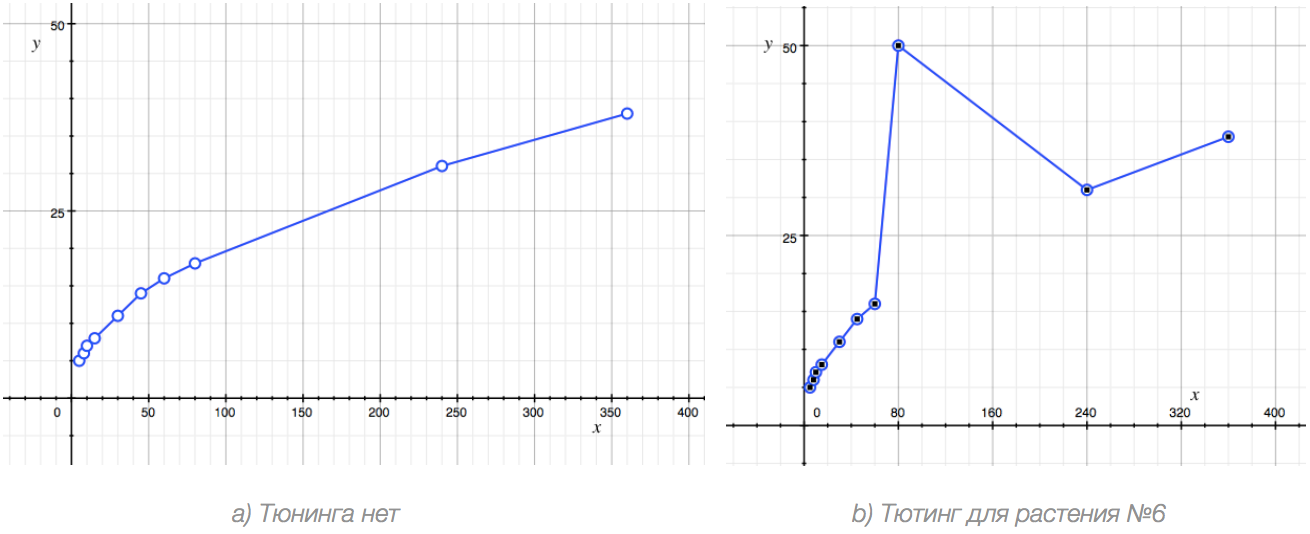
假设我们发现玩家在第18级时遇到很大困难（例如，游戏金币不足），因此感到疲惫而离开，永远不会回来。我们通过简单的方式解决了这个问题——我们将18级（在我们的表中是编号6）的植物的出售价格人为提高到50，以便玩家获得一个强大的赚钱机制，并重新获得信心（这个例子当然是夸张的，但在展示目的上是合适的）。

下面是两张图表——原始的和经过手动调整的平衡所得到的。

右侧图表明显存在一处偏离总体法则的点。在这种情况下（实际上通常如此），为了不失去全局视野，排除这些点最为有益。如果在右侧图表中我们移除点(80, 50)并将相邻点连接成直线，便几乎能和左侧一样清晰地看到函数图形。

主要建议如下：不要被孤立数字所迷惑，不要害怕超出总体法则的高峰。尽可能将它们从讨论中排除，稍后再回到它们的推理上。

4. 各种类型的函数

因此，我们得到了表格分布，并且已经绘制了图形。这个图形我们在脑海中可以继续延展，从而理解眼前的是什么——一个函数。正如我所说，存在多种数学方法来进行逼近，但实战中，我们需要关注某种自然算法，以便不失去对我们正在做的事情的理解。

该算法的第一步是理解我们所看到的函数图形的类型。函数类型决定了其图形的基本形状，可以通过缩放系数（即我们在方程中引入的数字加数和乘数）对其进行修改（平移、压缩、拉伸）。

函数类型有很多不同的形式。有些复杂到即使从图形上来看也很难判断这是方程，而不是随机的点集。幸运的是，在99%的情况下，我们不会处理这样的函数。下面我将尝试列出最常用的函数类型，并展示它们的图形。在学习这一部分后，您应该不会在根据图形特征判断函数类型时遇到问题。

为了简单起见，在后文中我们将使用以下符号：

• 函数的参数用字母x表示；
• 函数的值用字母y表示；
• y = f(x)的表述表示变量y由某个方程定义，其中x作为参数；
• 字母a, b, c等表示常数，即某些进入f(x)方程且不依赖于x的数字。

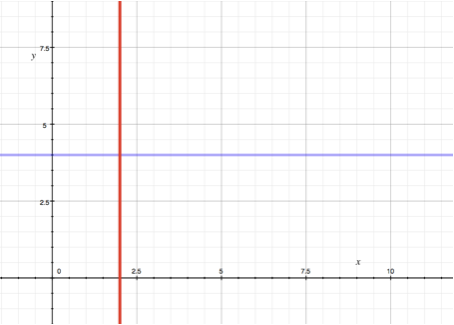
4.1. 常量函数

这是最简单的例子。在这样的函数方程中，x和y实际上并不相互依赖！

示例：y = 4, x = 2。

左侧的图形展示了两个函数。蓝色的由方程y = a定义（在这里，函数y在任意x值下取值a），而红色的由方程x = b定义（在这里，参数固定在值b，而y可以取任意值）。

实际上如果y = a，这意味着无论参数x如何，y都不会改变。例如，如果我们说玩家每分钟恢复的能量为1，和玩家的等级无关，这就是一个常量函数的例子。

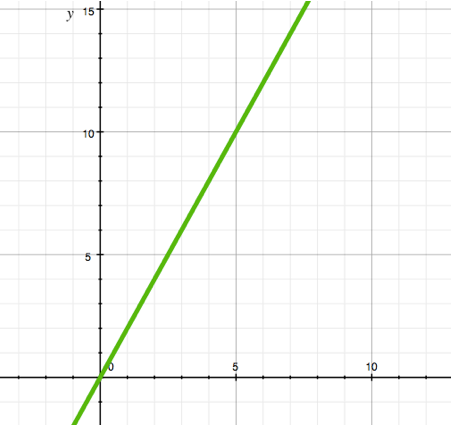
4.2. 线性函数

常规情况下，这类函数由方程y = a*x + b表示。

示例：y = x, y = 2*x + 3, y = 5-x。

这种函数的图形是一条直线，以某角度倾斜于坐标轴。图示中的函数y = 2*x，其图形通过坐标原点（因为当x = 0时，函数的值也为0）。总体上来说，这条直线并不一定要经过坐标原点。

线性函数的一个主要特点是保持恒定的增长速度（或在a < 0的情况下，保持恒定的减少速度）。想象一下，如果植物的出售价格线性与其生产时间有关。在这种情况下，可以表明，如果植物A的成熟时间是植物B的两倍，那么它的价格也将是植物B的两倍。简单法则由于其简单性常常用线性函数表达。例如，如果说玩家的最大能量是等级乘以三分之一，并每次向下取整为整数，那么每三等级最大能量就会增加1。

4.3. 幂函数

这一类型的函数包含若干子类型，便利地单独考察。每个这样的子型由同一个公式表示：y = k*xa + b，但由于a所在区间不同而各有差异。

a = 1, a = 0

如您所料，线性函数和常量函数是幂函数的特例。当a = 1时，我们有线性函数（y = k*x + b），而当a = 0时，我们有常量（y = k + b）。

a > 1

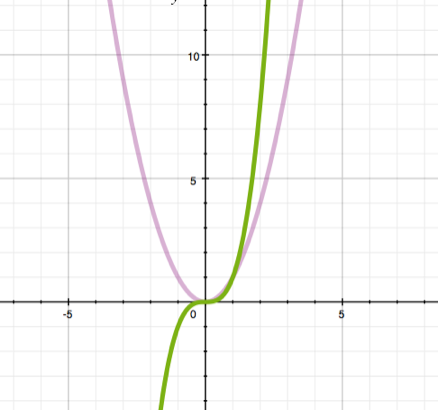
在这种情况下，函数图形是一条被称为抛物线的曲线。

示例：y = x3, y = 4*x3+3。

上图展示了函数y = x2（紫色曲线）和y = x3（绿色曲线）。通常我们只关注坐标空间的右上四分之一（在这里，y和x都是正的），但需要理解该类型函数在其他四分之一的行为差异。请注意，立方抛物线（绿色）在x小于零时向下，而平方抛物线（紫色）在同一区段上升。实际上，任意幂函数当a为偶数时，将永远不会取负值（因为负数x提升至偶数次方会给出正值），而奇数次幂的抛物线则可以取负值（例如，-3的三次方是-9）。

这种函数的特点在于，可以实现以递增的速度增长。通常，这类函数适用于游戏的难度增加、对玩家的要求增加或稀缺性的增加。显而易见的例子是，升级所需的经验值增加。开发者往往使用2或3作为这种增长的幂。另一个例子是在玩家等级上升的情况下，植物的成熟时间增加。如果植物A的解锁等级是植物B的两倍，那么其生产时间会是植物B的生产时间的两倍以上。

0 < a < 1

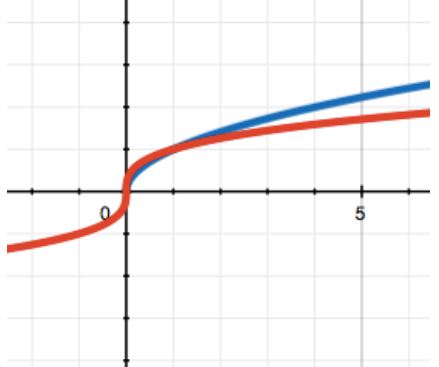
这种函数的图形像是一条以90度旋转的抛物线。

示例：y = √x, y = 2* x1/3。

图中展示了x的平方根（蓝色）和x的立方根（红色）。再次注意，在x < 0的情况下，函数的行为是不同的。负数平方根是未定义的，而立方根是存在的。

我们需要理解，x的平方根依然是幂函数。通过平方和平方根的例子可以清晰地展示这一点。因此，“x的平方”是x的二次幂，而“x的平方根”是x的1/2次幂。每次，幂的值可以表示为分数，其中分子是x的幂，分母是x的平方根的幂。因此x的2/3是x的平方的立方根。

值得注意的是，幂值本身决定了函数的增长速度。在a > 1的情况下，a越大，函数增长得越快（参见相关部分的图表，立方函数的增长快于平方函数）。在这里情况是一样的：1/2大于1/3，因此x的平方根将增长得比立方根更快。

此类函数在组织减缓游戏进度时是需要的。请看看我们在植物的销售价格取决于其成熟时间的表格示例中。出售价格随着时间的增加而上升，但这种增长是减缓的。基于表格获得的图形在形式上非常接近于根，是吗？

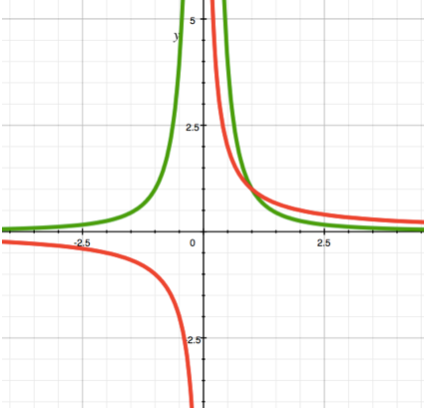
a < 0

理解负幂的意义非常简单。它仅表示参数位于分母。例如，记录y = x-3等同于记录y = 1/x3。

这样的函数图形被称为双曲线。

图中展示了a = -1（红色）和a = -2（绿色）的函数。再一次注意不同区域的函数行为差异。a = -1的函数存在于两个相反的象限（即y的符号要么总是与x相同，要么永远相反，取决于方程中的常数），而在a = -2的情况下，函数仅存在于一半（y的符号将永远是正的或负的，取决于方程中的常数）。

使用此类函数可以组织游戏内某个量的减少。请注意，这种减少的速度会随着时间的推移而减缓。

总结

幂函数在游戏设计中是最常用的。它们容易研究，能够以明确的速度组织增减的变化，且这种变化也容易控制。所有的幂函数子类型彼此紧密相关。例如，如果发现y等于x的平方，您可以大胆地声称（至少在正象限），x等于y的平方根。

幂函数有更一般的形式，称为n次多项式。其书写形式如下：y = kn * xn + kn-1 * xn-1 + kn-2 * xn-2 + … + k0 * x0。例如，4次多项式为y = 2*x4+ 1*x3 + x1 + 3。这里k2 = 0，因此我们没有遇到x的二次项。

实战中使用这种函数是合理的，因为它允许对平衡进行更精确和细致的调整（实际上，该公式具有更多的“杠杆”，可用于将平衡调整到某种方向），但这种更复杂的公式研究需要更深入的数学工具支持。

4.4. 指数函数

该函数可以写成y = k * ax的形式。此处参数不再是幂的底数（即被升幂的数），而是其指数（即显示我们将其提升到的幂的数）。常数则充当底数。

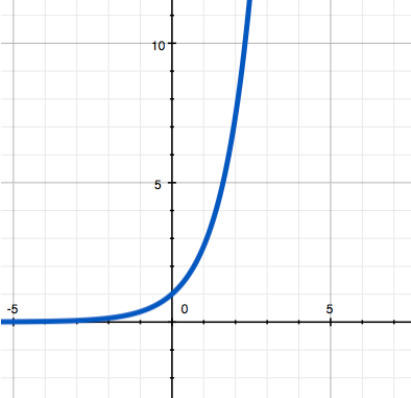
左侧图中盛行的“指数”函数是我们习惯认为的亚洲MMORPG平衡的代表。指数为y = ex，其中e是著名的特殊数字，拥有一系列突出的数学性质。其近似值为2.718281828（易于记忆——数字2和7后面跟着列夫·托尔斯泰的出生年份）。

该函数的图形外观上类似于抛物线，但增长（或者在a小于1时减少）速度显著更快。在小的a值（例如1.000000001）的情况下，指数函数增长速度较慢，但早晚也会追上任何一个幂函数。

当想要组织某个量的迅速增长时，会使用指数函数（在亚洲MMO中，此函数用于增加达到下一个级别所需的经验，以便快速减缓玩家通过等级的进度）。

4.5. 对数函数

在我的计算中，我不常使用对数函数，但这并不妨碍我在文章中提到它。若是在我们讨论的游戏的平衡中遇到它，我们应当准备好识别这一函数。

以a为底的x的对数，就是需要将a提升到的幂，以获得x。因此写表达式y = logax，就等同于说ay = x。

根据这一定义，得出结论，对数函数是指数函数的逆，即如果我们知道y是以a为底的x的对数，那么可以得到反法则：x是a的y次方。

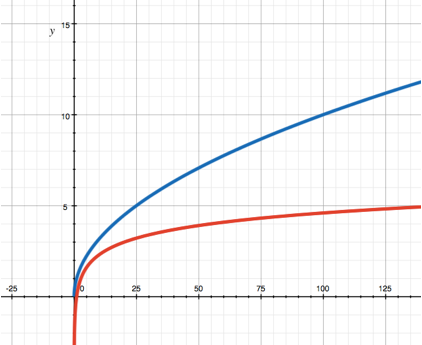
在图中，以e为底的对数（红色）与平方根（蓝色）进行了比较。最常用的对数有底数2（二进制）、e（线性）和10（十进制），底数越大，图形就越高。注意如果底数a < 1，则对数函数下降。

4.6. 三角函数sin和cos

在游戏平衡设计中也很少使用，但不提到它们会显得不公平。

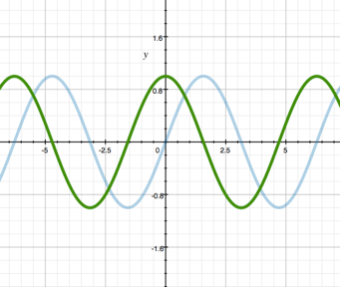
图中展示了y = sin(x)（蓝色）和y = cos(x)（绿色）的图形。它们的典型特征是周期性。在想要在游戏中组织周期性和重复性时可以使用它们。例如，如果您的游戏中有季节，那么作物产量（或国家的幸福感）可能会遵循类似的法则（夏季增长，冬季下降）。

显然，如果两个变量之间的关系是指数法则，那么对数函数就会出现。这个法则过于陡峭，通常不适合作为游戏平衡的基础。然而在想要“急剧收紧螺丝”的情况下，在游戏的后期阶段，例如，为了延长玩家耗尽全部内容再等待下一个游戏更新所需的时间，就可以使用它。我记得，早期暴雪在其魔兽世界中经常做到这一点。

结论和总结在文章的第二部分中。