Работа с кривыми LTV и ретеншена
Подробно о построении функций к таким метрикам, как LTV и ретеншен App2Top.ru рассказал генеральный продюсер студии «Овермайнд» Иван Игнатов. Осторожно: много формул.
Иван Игнатов
Постановка задачи
Большинство аналитических задач в области приобретения пользователей (User Acquisition) для игровых приложений, равно как и задач, связанных с экономическими расчетами в гейм-дизайне, так или иначе опираются на знание ключевых показателей проекта – кривой ретеншена и кривой LTV.
Кривая ретеншена r(t) – это функция, отражающая зависимость доли пользователей, оставшихся в проекте, от времени, прошедшего с момента их регистрации. Например, если на 7 день после регистрации в проекте остается 10,7% пользователей, а на 10 день – 8,8% то говорят, что ретеншен равен 0,107 и 0,088 соответственно. То есть r(7) = 0,107, r(10) = 0,088.
Кривая LTV – L(t) – это функция, отражающая средний доход с игрока в зависимости от времени с момента регистрации. Например, если за месяц с момента регистрации пользователи в среднем приносят по $2,55, то говорят, что «LTV 30 равен 2,55». То есть L (30) = 2,55.
Часто аббревиатурой LTV называют не саму функцию L(t), а значение дохода «за все время жизни пользователя», то есть L(∞). Поскольку это значение может быть известным только для очень давно существующих приложений, для которых уже поздновато заниматься анализом, на практике часто оперируют средним доходом за полгода или за год, то есть значениями L(182) или L(365). Например, фраза «трафик должен окупаться за полгода» означает требование L(182) ≥ CPI.
Во многих случаях необходимо построить аналитическое выражение r(t) или L(t), то есть «написать формулу» кривой, основываясь на имеющихся данных статистики проекта. Или, выражаясь математическим языком, аппроксимировать статистические данные аналитической кривой.
Примерами таких задач может быть:
- прогнозирование ретеншена и LTV на несколько месяцев вперед для проекта, еще не достигшего соответствующего возраста;
- оценка LT (Lifetime) среднего пользователя;
- оценка окупаемости рекламного трафика по результатам первых дней после старта рекламной кампании;
- построение гейм-дизайнером такой шкалы опыта по уровням, чтобы на всех уровнях было примерно одинаковое количество игроков;
Подход к задаче с нужной стороны
Когда аналитик сталкивается с необходимостью построения такой формулы или хотя бы с выбором из имеющихся на просторах интернета моделей, полезно иметь в виду следующее.
Существует множество банальных, осознаваемых каждым из нас истин, например, таких, как «все пользователи рано или поздно покинут проект», «среднее время жизни пользователя не может быть бесконечным», «чем больше времени с момента регистрации прошло, тем меньше доля оставшихся пользователей» или даже очевидное «в момент регистрации каждый пользователь активен».
Но далеко не каждая формула, не каждая модель, используемая для аппроксимации r(t) или L(t), выдерживает проверку на соответствие этим «банальным истинам».
Например, в качестве модели ретеншена иногда используют гиперболу:
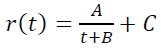
В качестве модели LTV также иногда используют так называемый «степенной тренд» L(t) = AtB, который попросту предполагает бесконечное ЛТВ, если рассматривать его «за все время жизни пользователя».
Это приводит к тому, что зачастую выбранная модель не может достаточно хорошо приблизить имеющиеся данные, или может на имеющемся временном промежутке, но начинает «дурить», когда ее «просят» сделать прогноз на несколько месяцев вперед.
Далее я описываю подход к «написанию формулы», опирающийся на изучение естественных свойств искомых функций. Суть его в том, чтобы выбрать из всего многообразия возможных формул именно те, свойства которых заранее совпадают с нашими эмпирическими представлениями о поведении аудитории проекта. Причем не только простейшим представлениям, «банальным истинам» но и более сложным. В частности, такому, как «чем дольше пользователь находится в проекте, тем меньше шанс, что он его оставит именно сегодня».
Связь между ретеншеном и LTV
Перед непосредственным решением задачи нужно заметить, что поиск вида кривой LTV можно свести к поиску вида кривой для ретеншена, то есть вместо двух разных задач рассматривать одну. Делается это следующим образом.
Производная L`(t) по времени от LTV имеет смысл накапливаемого дохода со среднего пользователя за единицу времени и по своей сути близка к кривой ретеншена r(t). Более того, при постоянном доходе за единицу времени с живого игрока А они просто пропорциональны друг другу: L`(t) = A r(t).
Величину A в маркетинге обычно называют ARPU (Average revenue per user, средний доход с пользователя). К сожалению, часто под ARPU понимают и другое. Например, L(30) сплошь и рядом называют «ARPU первого месяца». Но в рамках нашей работы мы будем под ARPU понимать именно среднюю величину дохода с живого игрока за единицу времени, и ничто иное.
Зачастую в первом приближении A предполагают постоянным, не зависящим от возраста пользователя, а значит L`(t) и r(t) меняющимися по одному и тому же закону. На практике оказывается, что это не так – в частности, не платящие пользователи бросают игру в среднем раньше, чем платящие, и поэтому A растет в зависимости от того, сколько пользователи уже играют, то есть от t. Другими словами, A = A(t) и L`(t) = A(t) r(t).
Однако даже в этом случае A(t) остается квазипостоянным, медленно меняющимся по сравнению с L`(t) и r(t), и это дает основания искать формулы их изменения в одном и том же семействе кривых.
Этот подход и применяется, и правомерность его подтверждается на практике тем, что получающиеся сглаженные L(t) достаточно близки к исходным эмпирическим кривым LTV рассматриваемых проектов.
Вывод искомых кривых
Итак, выводить мы будем r(t). Каком законам, каким «естественным свойствам» подчинен этот процесс?
Для начала выпишем те свойства, которые мы выше отнесли к «банальным истинам»:
1) r(0) = 100% = 1 (в момент регистрации все пользователи живы)
2) r(t) убывает на [0 ; ∞) (в среднем пользователи покидают игру)
3) ∫0∞ r(t) dt конечен.
Что это означает, «интеграл конечен»?
Допустим, на стабильный проект идет входящий стабильный трафик со скоростью N человек в единицу времени (в день).
Тогда в проекте игроков с возрастом от t до t+h получится N r(t) h , а всего живых игроков в проекте будет сумма всех этих величин по всей оси возраста игрока с шагом h, то есть:
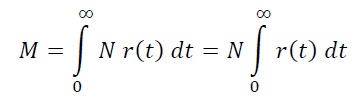
Кстати, отсюда на пальцах видно, что среднее время жизни пользователя:
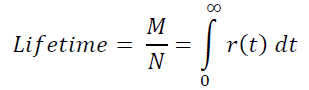
Свойствам 1) – 3) удовлетворяет простейшая элементарная функция r(t) = e-αt, a > 0.
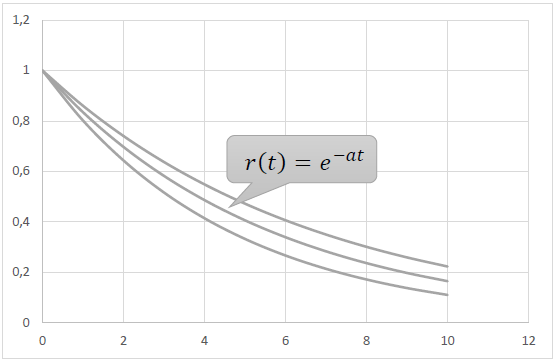
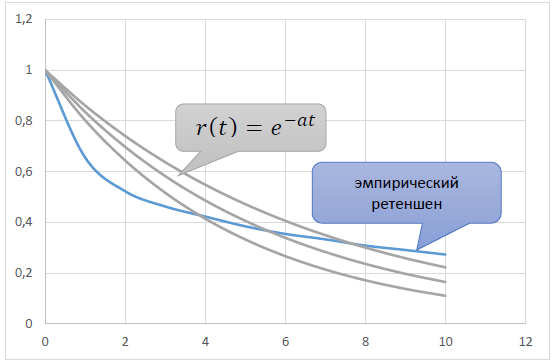
Такое поведение объясняется следующим эмпирическим свойством ретеншена:
4) Чем больше время с момента регистрации t, тем меньше «вероятность оттока» p(t) .
«Вероятность оттока» это вероятность того, что пользователь оставит игру за следующую единицу времени при условии того, что он раньше этого еще не сделал.
Как связаны между собой p(t) и r(t)?
Пусть мы имеем входной поток трафика N игроков в единицу времени, тогда до возраста t дожили N r(t) игроков, до возраста t+h дожили N r(t+h) игроков.
Следовательно, в интервале возраста [t ; t+h] теряется N r(t)− N r(t+h) игроков из N r(t) имеющихся. Значит, за h времени проект покидает доля игроков, равная
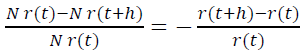
Нужно подчеркнуть, что под временем тут понимается субъективное время игроков, прошедшее с момента их регистрации, а не какой-то объективный общий для за всех интервал времени. Тогда за единицу времени проект покидает доля игроков, равная
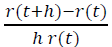
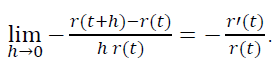
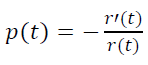
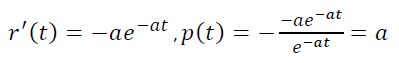
То есть модельная p(t) постоянна, а не убывает. Поэтому и наблюдается такое расхождение между эмпирическим r(t) и модельным r(t)=e-αt.
Попробуем обобщить модель так, чтобы p(t) убывало.
Возьмем p(t) = αtβ
- При β = 0 получаем уже рассмотренную модель p(t) = α , r(t) = e-αt
- При β < 0 получаем нужную нам убывающую вероятность оттока.
- При β > 0 получаем некое странное приложение с возрастающей по мере жизни игрока вероятностью оттока. Например, игру с жестко ограниченным по времени контентом.

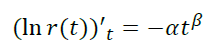
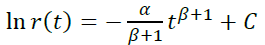
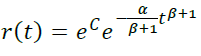
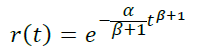
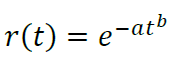
- β < 0 ⇔ b < 1 (убывание оттока, нормальный случай)
- β = 0 ⇔ b = 1 (постоянный отток, простая экспоненциальная модель)
- β > 0 ⇔ b > 1 (случай странного приложения с увеличивающимся оттоком)
Подбирая параметры a и b, исходя из требования близости теоретического r(t) к эмпирическому ретеншену, можно получить модельную кривую, достаточно точно отражающие реальную:
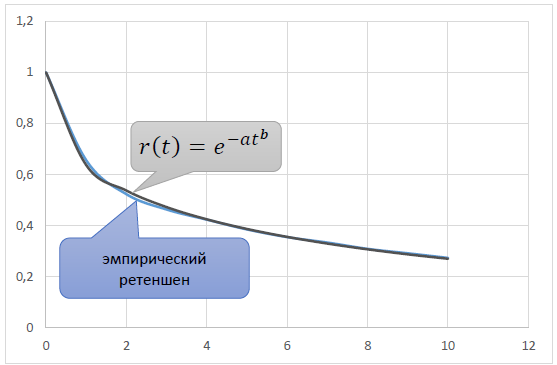
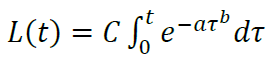
Замечание первое: про степенной тренд
Свойство 3), означающее конечность аудитории для r(t) и конечность LTV для L(t) выполняется только при β > −1 , то есть при b > 0.
Если рассмотреть ту же модель p(t) = αtβ при β = −1, получим:
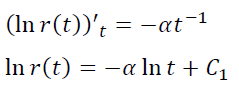
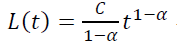
Вывод. Степенной тренд для кривой LTV, хотя и не удовлетворяет, в отличие от модели (**) условиям 1) и 3), все равно является ее краевым частным случаем при b → −1 с одновременным a → ∞ . А раз уж маркетологи применяют «степенной тренд» и считают его релевантным поведению кривой LTV, то более общую модель (**) и подавно можно считать релевантной.
Замечание второе: про увеличение числа параметров
Если аналитик располагает большим количеством статистических данных, у него может возникнуть желание подогнать к ним аппроксимационную кривую поближе, в надежде на то, что она даст в таком случае более точные прогнозы.
При этом он готов допустить в модель большее количество дополнительных параметров. Например, строить r(t) не двухпараметрическую, как наша модель (*), а трех-, четырех- или пятипараметрическую.
Как можно удовлетворить этому пожеланию, оставаясь в рамках построенной модели?
Можно моделировать смеси игроков. Например, считаем, что наш трафик состоит из смеси двух сортов пользователей с весами p и 1−p, и каждый сорт имеет свои параметры – a1,b1 и a2,b2 соответственно. Тогда получится:
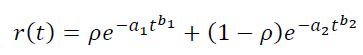
Аналогично можно увеличивать количество параметров в модели LTV:
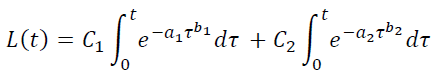
Однако привлекать многопараметрические модели нужно с большой осторожностью. Если параметров много, то аналитическая кривая может подстроиться под случайные выбросы, флуктуации статистики и задать тренды, которых на самом деле нет. В таком случае конечно многопараметрическая модель окажется ближе к статистическим данным, чем простая, но полученные по ней прогнозы и прочие выводы окажутся менее точными.
Поэтому прежде, чем пользоваться пятипараметрическйой моделью, имеет смысл пять раз хорошенько подумать, а надо ли оно вам.
Замечание третье: как пользоваться
Для практического применения найденных моделей нужно уметь две вещи. Брать интеграл вида (**) и находить оптимальный набор параметров a, b, C.
Интеграл этот не берется в элементарных функциях, но может быть выражен заменой переменных через Нижнюю неполную гамма-функцию γ(s,x), которую можно задать, например, в MS Excel, через реализованные в нем Гамма-функцию и Гамма-распределение такой формулой: =EXP(ГАММАНЛОГ(s))∗(ГАММА.РАСП(x,s,1,ИСТИНА)).
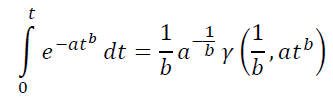
Таким образом, для использования предлагаемых моделей не требуется ни специального программного обеспечения, ни привлечения программистов.
На этом все. Надеюсь, вам было интересно. Если что-то вызвало вопросы – обязательно отпишитесь в комментариях.

